Random Binary Search Tree －Treap

BST插入顺序与平衡性

众所周知，二查搜索树(BST)的搜索、插入、删除的复杂度等于树高，所以平衡度越高，越接近$ O(nlogn) $，越有序越退化为$ O(n) $

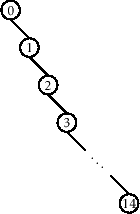
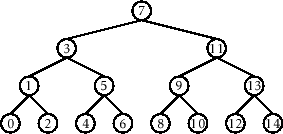
对于左侧的BST来说，只有唯一的构造序列：$ <1,2,\dots,14> $
但对于右侧的BST，可以存在21964800种不同序列

也就是说，随即插入序列到二叉树所形成的平衡度，将大于部分有序插入所形成的二叉树

形式化证明可以得到（具体证明过程，参见Open Data Structures：

对每个$ x \in{0,\ldots,{n}-1} $, x所需要的搜索长度（即深度）是 $ H_{x+1} + H_{n-x} - O(1) $

对每个$ x \in(-1,n) $，x所需要的搜索长度是$ H_{\lceil x \rceil} H_{n-\lceil x \rceil} $

Treap - Random BST实现

Treap-wikipedia

Treap，顾名思义，就是Tree和Head的结合体，除了要满足BST的要求外，还需要满足堆的要求，即

BST: 对每个结点，左子女的值 < 根的值 < 右子女的值
Heap: 对除了跟结点的每个结点，双亲结点的优先级要小于该结点的优先级

所以Treap的每个结点除了包括BST结点的值value外，还需要包括一个唯一的优先级p

比如这样就是一个典型的Treap，每个结点表示为(value,p)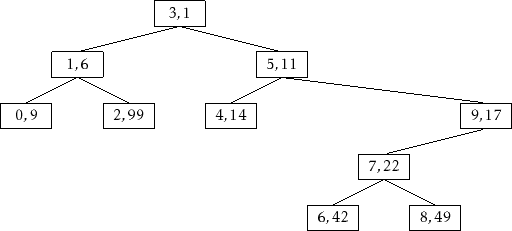

并且可以证明，由Heap的约束，最小优先级将成为根结点，而BST又保证了小于根的值将在左子树上，大于根的值在右子树

由于Heap的约束，我们可以认为Treap是按照优先级排序插入BST的，比如上述Treap可以由以下序列构造

$ (3,1), (1,6), (0,9), (5,11), (4,14), (9,17), (7,22), (6,42), (8,49), (2,99) $

旋转

为了确保Heap原则，那么就需要对树进行旋转，在旋转中同时还要确保BST原则，比如这样的例子：

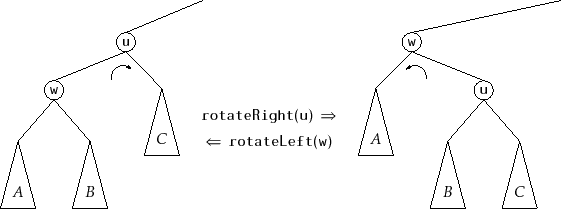
对w.value < u.value，旋转将交换w和u的父子关系，同时将把原来的B放在新的儿子上。比如右旋，可以看作左旋和右旋是一个对称的操作

void rotateRight(Node *u) {
    Node* w = u->left;
    w->parent = u->parent;  //parent -> w
    if (w->parent != NULL) {
        if (w->parent->left == u) { //u is left or right
            w->parent->left = w;
        } else {
            w->parent->right = w;
        }
    }
    u->left = w->right; //u.left = B
    if (u->left != NULL) {
        u->left->parent = u;    // B.parent = u
    }
    u->parent = w;  // w.right = u
    w->right = u;
    if (u == root) {   //if u is root
        root = w;
        root->parent = NULL;
    }
}

添加/删除

添加

比如，对上述的Treap，加入一个值1.5，生成的优先级为4，即插入结点为(1.5,4)。首先使用BST的Add，插入在(2,99)的左子女上。为了满足Heap规则，依次进行以下旋转：

99 > 4 =>右旋;
6 > 4 => 左旋;
1 < 4 => 停止;

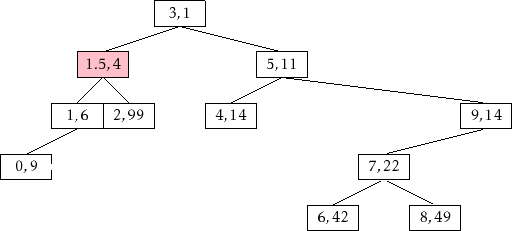
由前面的引理，可以知道，旋转的次数为$ 2ln(n) + O(1) $，复杂度为$ O(logn) $

删除

核心基本为添加的逆操作，对上述的Treap，删除一个结果(9)，那么将删除结点(9,17)。首先使用BST的Find，找到value为9的结点，然后将以(9,17)开始，向下不断旋转，直到最终为叶结点，然后把这个叶子剪去(Cut down)。

旋转原则：

left = NULL & right = NULL ，不动
left = NULL，左旋(right = NULL则右旋) 注:原文这里描述写反了
left.p < right.p，右旋(right.p < left.p则左旋)

依次进行以下旋转：

right = NULL => 右旋;
right = NULL => 右旋;
叶结点 => 停止;

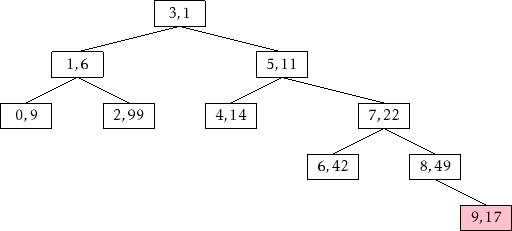
和添加相反，复杂度为$ O(logn) $

复杂度

构造: $ O(logn) $ 查找: $ O(logn) $ 添加: $ O(logn) $ 删除: $ O(logn) $

虽说都是$ O(logn) $，但是对比另一种高级数据结构Skip List(跳表)，查找复杂度在常数上有不同：

Skip List: $ elnn + O(1) \approx 1.884log(n) + O(1) $ Treap: $ 2ln(n) + O(1) \approx 1.386log(n) + O(1) $

代码

完整版C++实现，这里面的随机优先级，直接使用了value当种子srand()然后rand()获取随机数……（先进行BST的Add，确保value不会重复），实际中可以采用其他随机数方式获得更好的期望复杂度（吐槽……开始没注意这是Java版伪代码，以后一定用Java或者JavaScript写……指针地狱）

代码链接：Treap