Core Animation 3D 仿射变换知识

之前写的Core Graphics是2D平面上的坐标变换，而iOS开发中，为了实现复杂的动画效果，视图切换效果，会用到很多3D变换，这就是Core Animation提供的CATransform3D，其中大部分API都和2D情况类似，但这里需要详细解释一下透视投影这个概念，和m34这个值的真实来源，一些博客抄来抄去却没有点到点子上，让人看不下去……

变换矩阵

typedef struct CATransform3D {
  CGFloat m11, m12, m13, m14;
  CGFloat m21, m22, m23, m24;
  CGFloat m31, m32, m33, m34;
  CGFloat m41, m42, m43, m44;
} CATransform3D;

这个结构体对应的是这样一个4x4的变换矩阵：

$ \begin{bmatrix} m11 & m12 & m13 & m14 \\ m21 & m22 & m23 & m24 \\ m31 & m32 & m33 & m34 \\ m41 & m42 & m43 & m44 \end{bmatrix} $

矩阵定义的顺序和结构体一致，先行后列（注意，那个《Core Animation Advanced Techniques》矩阵的图是错误的，行列画反了），则对应的矩阵乘法为

$ \begin{bmatrix} x & y & z & 1 \end{bmatrix} \times \begin{bmatrix} m11 & m12 & m13 & m14 \\ m21 & m22 & m23 & m24 \\ m31 & m32 & m33 & m34 \\ m41 & m42 & m43 & m44 \end{bmatrix} = \\ \begin{bmatrix} m11x+m21y+m31z+m41 & m12x+m22y+m32z+m42 & m13x+m23y+m33z+m43 & m14+m24+m34+m44 \end{bmatrix} $

注意：

这里定义的向量最后一位表示齐次向量元素，如果不为1，需要再化为齐次坐标（通常情况可以取m14,m24,m34,m44为0,0,0,1），对应真正的x,y,z坐标

$ \begin{bmatrix} \frac{m11x+m21y+m31z+m41}{m14+m24+m34+m44} & \frac{m12x+m22y+m32z+m42}{m14+m24+m34+m44} & \frac{m13x+m23y+m33z+m43}{m14+m24+m34+m44} \end{bmatrix} $

iOS设备上，是按照左手系的三维空间，即正面面对设备屏幕，坐标原点从屏幕左上方起，x轴指向右方，y轴指向下方，z轴为屏幕指向眼球。而macOS上是右手系，原点是屏幕左下角，x轴指向右方，y轴指向上方（相反），z轴同样为屏幕指向眼球，要注意

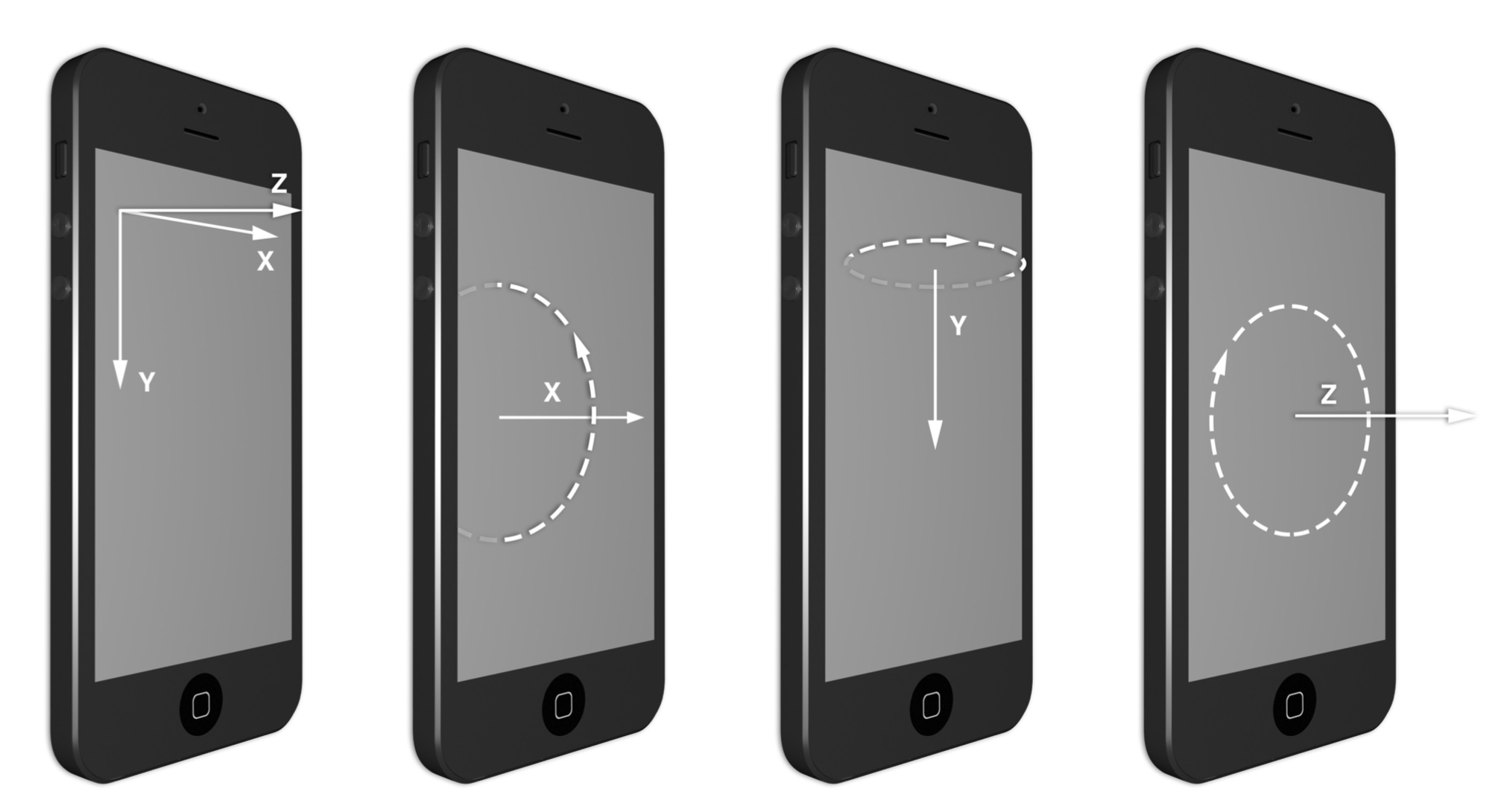
平移

类似二维空间的平移，变换矩阵第四行的m41,m42,m43对应的就是x、y、z的平移量，因此矩阵变换很简单，比如将[x,y]向量平移到[x+a,y+b,z+c]：

平移矩阵：
$ \begin{bmatrix} x & y & z & 1 \end{bmatrix} \times \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ a & b & c & 1 \end{bmatrix} = \begin{bmatrix} x+a & y+b & z+c & 1 \end{bmatrix} $

对应构造API：

1	CATransform3D CATransform3DMakeTranslation(CGFloat tx, CGFloat ty, CGFloat tz);

缩放

同二维空间的缩放，我们需要对向量坐标乘以系数，那么构造出来一个对角矩阵即可

缩放矩阵：

$ \begin{bmatrix} x & y & z & 1 \end{bmatrix} \times \begin{bmatrix} a & 0 & 0 & 0 \\ 0 & a & 0 & 0 \\ 0 & 0 & a & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} ax & ay & az & 1 \end{bmatrix} $

对应的构造API：

1	CATransform3D CATransform3DMakeScale(CGFloat sx, CGFloat sy, CGFloat sz);

旋转

参考二维的旋转，二维的旋转我们讨论的是某个layer，以它自身的anchorPoint为原点，通过顺时针逆时针的旋转。但是对于三维来说旋转就麻烦了，因为向量不会仅仅在XoY平面上。虽然实际上可以定义绕任意轴旋转，但是一般我们只研究绕三个坐标轴（x,y,z）的旋转。其中，对于绕z轴的旋转，可以看作等价于二维的旋转（XoY平面内），但绕x和绕y就超出了屏幕

对于绕坐标轴，我们可以把对应旋转平面的投影看成二维的情况，因此前面推导过的旋转矩阵同样适用于三维绕轴情况，只需要针对不同坐标轴选定不同的坐标罢了，即通过把前一篇推导方程替换x，y，z变量得到：

$ \begin{cases} x^{‘} = x \cos \theta - y \sin \theta \\ y^{‘} = y \cos \theta + x \sin \theta \\ z^{‘} = z \end{cases} $

绕x轴的旋转矩阵（固定x，从y旋转到z，即用y替换x，z替换y，x替换z）：

$ \begin{bmatrix} x & y & z & 1 \end{bmatrix} \times \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos \theta & \sin \theta & 0 \\ 0 & - \sin \theta & \cos \theta & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} x & y \cos \theta - z \sin \theta & z \cos \theta + y \sin \theta& 1 \end{bmatrix} $

绕y轴的旋转矩阵（固定y，从z旋转到x，即用z替换x，x替换y，y替换z）：

$ \begin{bmatrix} x & y & z & 1 \end{bmatrix} \times \begin{bmatrix} \cos \theta & 0 & - \sin \theta & 0 \\ 0 & 1 & 0 & 0 \\ \sin \theta & 0 & \cos \theta & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} x \cos \theta + z \sin \theta & y & z \cos \theta - x \sin \theta & 1 \end{bmatrix} $

对应API：

1	CATransform3D CATransform3DMakeRotation(CGFloat radians, CGFloat x, CGFloat y, CGFloat z);

注意：这个API中，radians是弧度不用说，x,y,z分别介于[-1,1]之间，表示一个任意的单位向量（[x,y,z]的长度是1，比如设置[1,0,0]就指的是绕x轴正方向旋转对应弧度值，前面解释过iOS和macOS的正/负弧度对应顺/逆时针了）

错切

类似二维的情况，比如对z轴依赖不变，x和y线性变换，那么对应的就是m12和m21，也是没有专门的API，用CATransform3DIdentity 便携初始化结构体创建一个吧，设置对应的矩阵值即可

错切矩阵：

$ \begin{bmatrix} x & y & z & 1 \end{bmatrix} \times \begin{bmatrix} 1 & m21 & 0 & 0 \\ m12 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} x+m12y & m21x+y & z & 1 \end{bmatrix} $

手动构造API：

//The identity transform: [1 0 0 0; 0 1 0 0; 0 0 1 0; 0 0 0 1]
CATransform3DIdentity transform = CATransform3DIdentity;
transform.m12 = 1.0;
transform.m21 = 1.0;

透视投影

实际中你如果直接使用旋转，会注意到旋转前后，结果看起来竟然和普通的缩放一模一样，这是为什么呢？原因其实很简单，假如绕y轴旋转，空间中的图层虽然旋转了，但是显示到XoY平面（也就是iPhone的屏幕上）的时候，会把3D的物体进行正投影，这样子看上去就像是左右压缩一样

而学过绘画的都知道人的视野并不是平行的，而是有一个透视图的概念，眼睛前有实际平行的两条线段发出（相当于z轴方向的向量），人眼看起来会相交于一点上（焦点，Focal point），这才产生了3D感

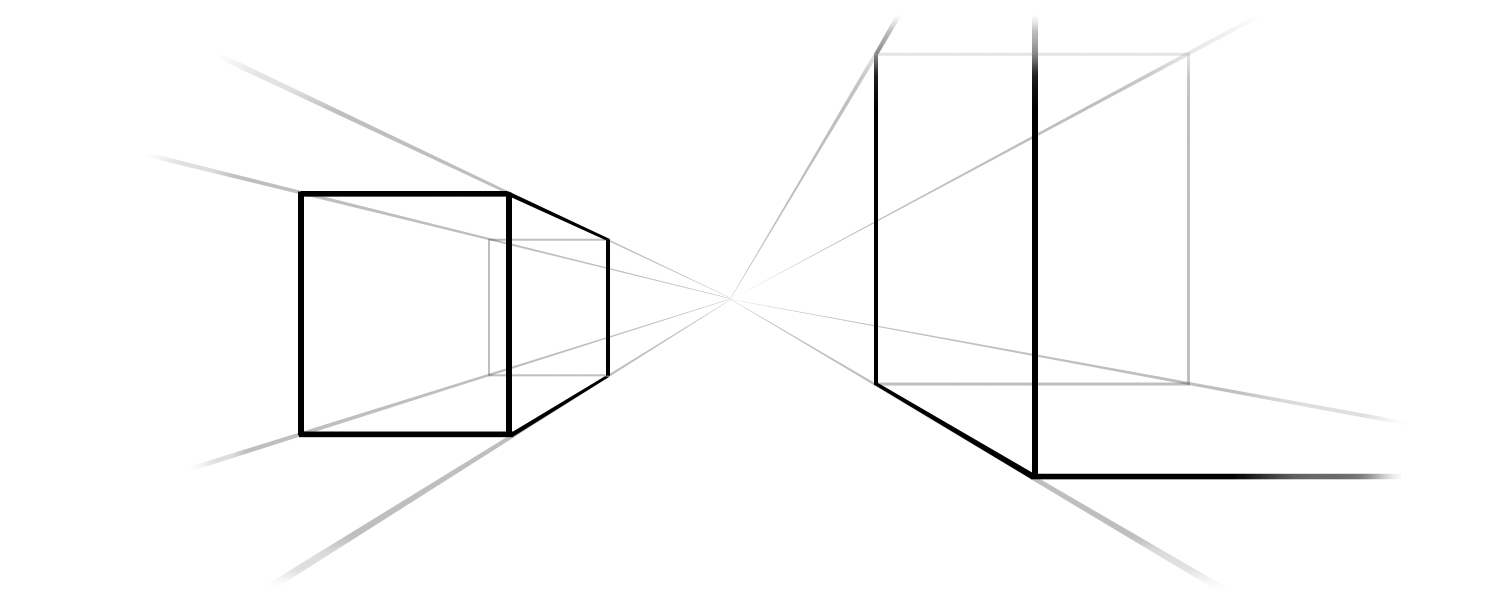
而对于变换矩阵，如果要实现透视投影，应该怎么办？这里就用到了前面介绍过但一直忽略的值m34

原理和推导：

为什么单单修改一个m34的值，就能达到这种透视3D的效果呢？我简单看了很多类似的博客都没有正面回答这个问题，其实这是变换矩阵的透视投影结论，可以通过简单的数学推导得到

Core Animation已经定义了焦点的x,y坐标，就是这个图层的anchorPoint（锚点），同时取z=0的XoY平面作为图像平面（也就是iPhone的屏幕平面），那么假如我希望投影中心到图像平面的距离是d，可以假设焦点坐标为(0,0,d)，现在对m34的值进行赋值为w，初始向量坐标为(x,y,z)，开始推导：

矩阵乘法：

$ \begin{bmatrix} x & y & z & 1 \end{bmatrix} \times \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & w \\ 0 & 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} x & y & z & zw+1 \end{bmatrix} $

此时得到的向量不为齐次，需要进行齐次化，得到真正的坐标：

$ \begin{bmatrix} x^{‘} & y^{‘} & z^{‘} \end{bmatrix} = \begin{bmatrix} \frac{x}{zw+1} & \frac{y}{zw+1} & \frac{z}{zw+1} \end{bmatrix} $

最后对XoY平面进行投影，则最终看到的二维向量应该为$ (\frac{x}{zw+1}, \frac{y}{zw+1}) $

现在考虑x轴的情况（y轴同理），我们知道真实三维空间的x坐标是x，
现在得到透视投影下的x坐标是x/(zw+1)

为了得到d和w的关系，这里引用一幅图，绿色的点为原始点，红色的点为投影到XoY平面上的点，我们这里推导不需要管具体的值，只是为了更清晰地发现规律：

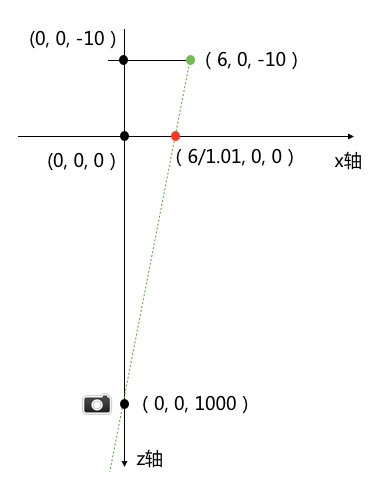
$ \because 由图，依据相似三角形原理 \\ \therefore \left| \frac{x}{zw+1}: x \right| = d : (\left|z\right|+d) \\ 去绝对值号，且d\neq0,x\neq0，得 \\ \frac{1}{zw+1} = \frac{1}{1-\frac{z}{d}} \\ \therefore w = - \frac{1}{d} $

这样就得到重要的结论：w=-(1/d)，即，假定焦点（就是人眼）距离原点距离为d，则m34应当填写-(1/d)

默认初始变换矩阵的m34都是0，也就是说认为焦点无限远，因此看起来没有任何3D感。同时，我们也知道，假如我们取d越大，则看起来越没有投射和3D感；取d越小，则3D感和失真感越强烈，一般推荐的d值在500~1000之间，也就是说m34填写-1/500即可

设置变换矩阵的m34：

CATransform3D transform = CATransform3DIdentity;
//apply perspective
transform.m34 = - 1.0 / 500.0;
//rotate by 45 degrees along the Y axis
transform = CATransform3DRotate(transform, M_PI_4, 0, 1, 0);
//apply to layer
self.layerView.layer.transform = transform;

总结

Core Animation提供的CATransform3D主要的几个变换都在这里介绍了，尤其是透视投影，一定要理解原理，知道为什么需要修改m34来控制透视焦点。

当然，实际上CATransform3D主要用来作各种3D动画效果，比如你可以自定义一个View的转场效果，搞个3D相册，甚至可以在不需要接触OpenGL的情况下写个小游戏（比如魔方啊之类），对于iOS进阶非常有帮助。最近有点忙没太关注，感觉自己还是需要学习一个。

参考资料

iOS Core Animation Techniques

iOS的三维透视投影

小猪的博客

Core Animation 3D仿射变换知识

Core Animation 3D 仿射变换知识

变换矩阵

平移

缩放

旋转

错切

透视投影

原理和推导：

总结

参考资料